Quem toca piano aprecia, ainda que não tenha consciência disso, a beleza da função exponencial.  A altura de uma nota musical é dada pela frequência da nota musical.  O Lá acima do Dó médio no piano, por exemplo, corresponde a uma vibração de 440 hertz. Uma nota uma oitava acima deste Lá vibra a 880 hertz, e uma nota uma oitava abaixo deste Lá vibra a 220 hertz.

   Considere $n$ o número inteiro de oitavas acima ou abaixo deste Lá e $V = f(n)$ o número da frequência da nota correspondente ao valor de $n$. Quando o número de oitavas estiver acima, consideraremos $n \gt 0$, quando estiver abaixo, consideraremos $n \lt 0$. Assim, tem-se $f(0) = 440$, $f(1) = 880$ e $f(\mbox{-}1) = 220$. A tabela abaixo nos fornece outros valores para a função $f$.

   Observe que $... = \displaystyle\frac{f(4)}{f(3)} = \displaystyle\frac{f(3)}{f(2)} = \displaystyle\frac{f(2)}{f(1)} = \displaystyle\frac{f(1)}{f(0)}= \displaystyle\frac{f(0)}{f(\mbox{-}1)}= \displaystyle\frac{f(\mbox{-}1)}{f(\mbox{-}2)}= \displaystyle\frac{f(\mbox{-}2)}{f(\mbox{-}3)} = ... = 2$; isto é,

$f(n)$ é uma progressão geométrica de razão 2. 

   Tal fato sugere que $V$ seja uma função do tipo exponencial em relação a $n$, quer dizer: $f(n) = k \cdot 2^{n}$.

   Para encontrarmos o valor de $k$ basta usarmos o dado $f(0) = 440$ da tabela:

$440 = f(0) = k \cdot 2^{0} = k$

   Logo $V = f(n) = 440 \cdot 2^{n}$. Eis a função exponencial que é responsável pelas oitavas musicais do Lá.

   Substâncias radioativas perdem uma porcentagem de sua massa a cada unidade de tempo.  O período de tempo em que a massa de uma certa substância radioativa fica reduzida à metade do seu valor inicial é denominado meia-vida da substância.

   O urânio e o carbono-14 são duas das substâncias radioativas mais conhecidas. Esta última, por exemplo, é usada para datar objetos orgânicos. Um osso ou uma parte de um organismo vivo acumula pequenas quantidades de carbono radioativo 14. Quando o organismo morre, não recolhe mais carbono-14 por interação (por exemplo, a respiração) com o seu ambiente. Assim, medindo a proporção de carbono-14 em uma parte do organismo morto, e comparando com a proporção da mesma parte em um organismo vivo, pode-se determinar a quanto do carbono-14 original decaiu, e desse modo, fazer uma estimativa do tempo em que ocorreu a morte do organismo.  Entendeu? Quer experimentar o método? Vamos ao problema, quer dizer, a uma aventura arqueológica!

Sabe-se que a quantidade, $Q$, de carbono-14 radioativo que permanece no organismo $t$ anos após a morte é dada por $Q = Q_{0} \cdot e^{0\mbox{,}000121t}$. Você seria capaz de avaliar a idade de um crânio descoberto numa escavação arqueológica e que apresentava em sua composição apenas 15% da quantidade original de carbono-14? Quer saber a resposta? Clique no crânio da figura ao lado e veja a solução. Mas, antes, tente descobrir por você mesmo!    Resposta: 15678,7 anos

MATEMÁTICA FINANCEIRA E FUNÇÃO EXPONENCIAL:
O INÍCIO DE UMA GRANDE AVENTURA.

Tendo como base a pesquisa que realizou para escrever seu belo texto “$e$: a história de um número”, Eli Maor revela-nos que o número irracional $e$ (base da nossa função exponencial) surgiu pela primeira vez em um trabalho de John Napier sobre logaritmos, publicado em 1618. Neste trabalho, o número $e$ estaria associado a uma fórmula para o cálculo de juros compostos.    Mas, que fórmula é essa?

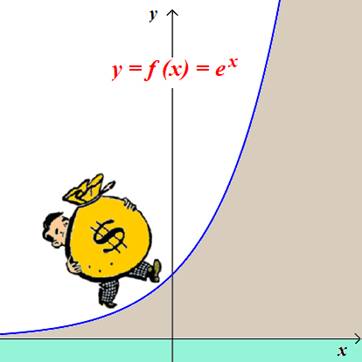
   Vejamos, se um capital $P$ é composto $n$ vezes por ano, durante $t$ anos, a uma taxa anual de juros $r$, o capital $S$ ao final de $t$ anos será expresso pela fórmula

$S = P \cdot \left(1 + \displaystyle\frac{r}{n}\right)^{nt}$.

   Para melhor entendermos nossa fórmula, consideremos $P$ igual a 1 real, $t$ igual a um ano e a taxa de juros $r$ igual 100%. Uau! Quem não gostaria de receber 100% de juros sobre sua aplicação durante um ano? Mas esta hipótese é apenas matemática (e didática), foge completamente nossa realidade atual de míseros 0,5% ao mês, não é mesmo?

   Voltemos a nossa fórmula, agora com forma mais simplificada, pois $r = 1$, $P = 1$ e $t =1$.

   Suponha agora que a taxa de juros de 100% seja aplicada apenas ao final de um ano, ao término do empréstimo. Neste caso, $n$ também é igual a 1 e $S = 1 \cdot \left(1 + \displaystyle\frac{1}{1}\right)^1 = 2$. Isto é, a nossa moeda de 1 real teria rendido outra moeda de 1 real. Nosso capital que era de 1 real tornou-se, após um ano, igual a dois reais (dobramos nosso capital! Isso parece um bom negócio!).

   Suponha agora que a taxa de juros de 100% seja aplicada em duas etapas, quer dizer, semestralmente: 50% ao final de seis meses e mais 50% ao final do empréstimo.

   Neste caso $S = \left(1 + \displaystyle\frac{1}{2}\right)^{2} = 2\mbox{,}25$; isto é, em vez de dois reais, teríamos dois reais e vinte e cinco centavos. Se já estava bom, ficou ainda melhor!

   E se a taxa fosse composta bimestralmente, quer dizer, 6 vezes ao ano?

   Neste caso $S = \left(1 + \displaystyle\frac{1}{6}\right)^{6} = 2\mbox{,}5216263717421124828532235939643...$, quer dizer, receberíamos ao final de um ano, dois reais e cinquenta e dois centavos (como o banqueiro não é matemático, colocaria o restante dos dígitos decimais no próprio bolso). Melhorou, não é mesmo?

   Se a taxa de 100% fosse composta mensalmente? Ficou curioso, né? Confira as contas.

   $S = \left(1 + \displaystyle\frac{1}{12}\right)^{12} = 2\mbox{,}6130352902246781602995330443549...$, isto é, $S$ seria aproximadamente dois reais e sessenta e um centavos.

   Você deve está observando que à medida que $n$ cresce, o nosso saldo está aumentando.  Continuemos então a aumentar o valor de $n$. Isso é muito bom!

   Considere agora $n = 365$, isto é, nossa taxa será composta diariamente:

   $S = \left(1 + \displaystyle\frac{1}{365}\right)^{365} = 2\mbox{,}7145674820218743031938863066851...$, que seria aproximadamente igual a  dois reais e setenta e um centavos. Isto parece não ter fim, não é mesmo?

   Abstraindo de vez e viajando para o mundo matemático (fique tranquilo – como diria Platão –  lá, tudo é perfeito!), construiremos uma tabela que nos mostrará até onde isso vai.

   E aí, os valores de $S(n)$ continuam crescendo. Mas ao olhar para a tabela, você deve ter percebido que o valor 0,7182 parece estar consolidado nas quatro primeiras casas decimais dos valores de $S(n)$ que aparecem a partir da oitava linha. No entanto, a sensação que temos é que a sequência de valores $S(n)$ parece não ter fim, não é mesmo? Mas isso é só sensação. Isso passa, tão logo você conheça o mundo da Análise Matemática. Não é o caso aqui, mas é possível provar que os valores desta sequência $S(n)$ têm um limite quando fazemos $n$ tender ao infinito. E este ponto limite é, por definição, o número irracional $e$ (número de Euler). Este número é irmão (mais novo) de outro número irracional que você já ouviu falar: o $\pi$. A representação decimal de $\pi$, assim como de qualquer número irracional, também é infinita e não periódica.  Assim, podemos sintetizar essa nossa conversa  em notação matemática compacta do seguinte modo: $e = \lim_{n \rightarrow \mbox{+}\infty} \left(1 + \displaystyle\frac{1}{n}\right)^{n}$.

A IDENTIDADE DE EULER

Existe uma fórmula famosa – talvez a mais compacta e famosa entre todas as fórmulas – desenvolvida por Euler a partir de uma descoberta de De Moivre: $e^{i\pi} + 1 = 0$. ... Ela fascina igualmente o místico, o cientista, o filósofo e o matemático. - Edward Kasner e James Newman, Mathematics and the Imagination (1961)    Leonahrd Euler (1707-1783) foi um grande matemático suíço. Nasceu em 15 de Abril de 1707, em Basileia.  Foi com certeza um dos matemáticos mais produtivos que a humanidade já conheceu. Estima-se que sua imensa contribuição intelectual ultrapassaria mais de setenta volumes.  Euler passeou pelos mais diversos campos da matemática (cálculo, álgebra, teoria dos números, geometria, topologia, análise complexa, etc). Alguns símbolos matemáticos herdamos desse grande mestre, entre eles, $\pi$, $i$, $e$ e $f(x)$. Com relação aos três primeiros listados acima, recebemos, por volta de 1750, uma das mais maravilhosas e das mais enigmáticas expressões matemáticas, a Identidade de Euler:

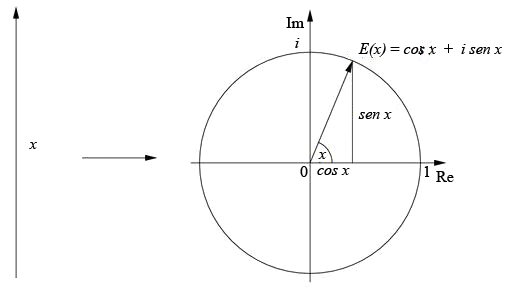
$e^{i\pi} + 1 = 0$

   A identidade de Euler contém os dois números irracionais transcendentes mais famosos da história da matemática, um número imaginário e os dois números inteiros essenciais para o mundo digital.  A expressão é um caso particular de uma outra relação descoberta pelo matemático, a equação de Euler:

$e^{ix} = \mbox{cos}x + i\mbox{sen}x$, qualquer que seja $x \in $ IR.

   De fato, faça $x = \pi$ na equação e obteremos a expressão de Euler.

$e^{i\pi} = \mbox{cos}\pi + i\mbox{sen}\pi = \mbox{-}1 \Leftrightarrow e^{i\pi} + 1 = 0$

   Para a descoberta da relação $e^{ix} = \mbox{cos}x + i\mbox{sen}x$, Euler fez uso de uma função auxiliar que recebe hoje, em sua homenagem, o seu nome. A função de Euler é uma função complexa $E : $ IR $ \to S^{1} \subset \mathbb{C}$, que associa um número real $x$ ao número complexo $E(x) = \mbox{cos}x + i\mbox{sen}x$, cuja representação encontra-se no círculo unitário $S^{1}$ com centro na origem.

   Observe que

   Observou alguma coisa de interessante na função de Euler? Não?

   Vê se você observa alguma semelhança com a propriedade da função exponencial a seguir:

$e^{(x + y)} = e^{x}e^{y}$

   Isso mesmo, a função complexa de Euler se comporta algebricamente como a função exponencial real $f(x) = e^{x}$.

   Pois bem, foi este momento de inspiração que levou Euler a definir $e^{ix}$ por $\mbox{cos}x + i\mbox{sen}x$.

   Pode-se chegar a esta fórmula por outros caminhos. Mas isso é o que menos importa aqui em nossa conversa. Por enquanto, é suficiente que você aprenda a admirá-la.  Os cinco números que aparecem na fórmula representam quatro grandes áreas da matemática clássica: a aritmética representada pelo 0 e pelo 1, a álgebra pelo número imaginário $i$, a geometria pelo $\pi$ e a análise (cálculo) pelo $e$. Nessa expressão matemática está consolidada grande parte da história da própria matemática. Ave Euler!!!

A ESPIRAL LOGARÍTMICA

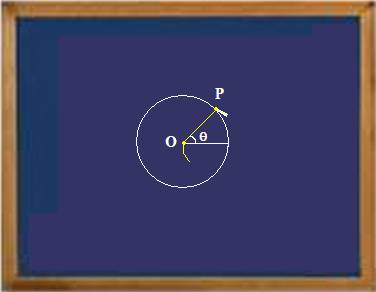
   Para desenharmos um círculo no quadro de giz podemos usar um barbante e um pedaço de giz.

   Primeiro amarramos o bastão de giz em uma das extremidades do barbante.

   Em seguida, esticamos o barbante, fixando a outra extremidade no quadro (ponto $O$ da figura abaixo) e giramos a ponta em que se encontra o bastão de giz em torno do ponto fixo $O$. O ponto $O$ é o centro do círculo. Observe que a distância de qualquer ponto $P$ do círculo ao ponto $O$ é constante. Denominamos esta constante de raio do círculo. Se considerarmos $r$ como sendo a medida do raio, conclui-se que a função que associa cada ângulo $\theta$ (veja figura abaixo) a medida $r = r(\theta)$ é constante.

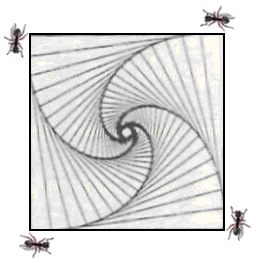
   Imagine agora que, ao repetir o movimento anterior, você deixa o barbante escorregar lentamente no ponto $O$. Isto é, à medida que você vai aumentando o valor de $\theta$, o valor do raio $r(\theta)$ também está aumentando. O desenho que você irá desenhar no quadro se assemelha ao da figura a seguir. Esta curva plana é denominada espiral. 

   Quando a função $r(\theta)$ é do tipo exponencial ($r(\theta) = e^{a\theta}$), a curva é denominada por espiral logarítmica (a palavra logarítmica está associada à forma antiga e equivalente de se representar a equação desta curva: $\mbox{ln(}r\mbox{)} = a\theta$). A figura do desenho anterior foi feita com um software matemático e  é uma espiral logarítmica.

   A espiral logarítmica tem propriedades matemáticas notáveis. E, por conta dessas propriedades, essa família de curvas tem despertado o interesse não só de matemáticos, mas também de artistas e cientistas de outras áreas do conhecimento. Observe que esta curva parece a mesma em todas direções. Melhor dizendo, cada semirreta com origem no polo (ponto $O$) atravessa a espiral exatamente com o mesmo ângulo. Por isso a espiral logarítmica também é conhecida como espiral equiangular.

   A spira mirabilis,  como a chamava o matemático Jakob Bernoulli, ocorre com espantosa frequência na natureza. Podemos observá-la, por exemplo, tanto na concha do náutilo bem como na forma de algumas galáxias.

   Deixamos agora um desafio interessante.

   Imagine quatro insetos posicionados nos cantos de um quadrado. Ao tocar um apito, cada inseto começa a se mover em direção ao seu vizinho. Quais são as trajetórias dos insetos e onde eles irão se encontrar? 

   Clique aqui para ver a resposta.

   Desenvolveremos a caracterização da função exponencial de dois modos: primeiro, usando a noção de acréscimo relativo (Teorema 1), e depois, a partir da relação existente entre esta função e as sequências numéricas (progressões aritméticas e geométricas) que você estudou no ensino médio (Teorema 2).

Teorema 1 (Caracterização das funções de tipo exponencial.)

   Seja $g : $ IR $ \to $ IR₊ uma função monótona injetiva (isto é, crescente ou decrescente) tal que, para $x$, $h \in $ IR quaisquer, o acréscimo relativo $\displaystyle\frac{g(x + h) - g(x)}{g(x)}$ dependa apenas de $h$, mas não de $x$. Então, se $b = g(0)$ e $a = \displaystyle\frac{g(1)}{g(0)}$, tem-se $g(x) = ba^{x}$ para todo $x \in $ IR.

Demonstração: Como vimos acima, a hipótese feita equivale a supor que $\phi(h) = \displaystyle\frac{g(x + h)}{g(x)}$ independe de $x$. Substituindo, se necessário, $g(x)$ por $f(x) = \displaystyle\frac{g(x)}{b}$, onde $b = g(0)$, $f$ continua monótona injetiva, com $\displaystyle\frac{f(x + h)}{f(x)}$ independente de $x$ e, agora, com $f(0) = 1$. Então, pondo $x = 0$ na relação $\phi(h) = \displaystyle\frac{f(x + h)}{f(x)}$, obtemos $\phi(h) = f(h)$ para todo $h \in $ IR. Vemos assim que a função monótona injetiva $f$ cumpre $f(x + h) = f(x) \cdot f(h)$, ou seja $f(x + y) = f(x) \cdot f(y)$ para quaisquer $x, y \in $ IR. Segue-se então* que $f(x) = a^{x}$, logo $g(x) = b \cdot f(x) = ba^{x}$, como queríamos demonstrar.

(*) A passagem assinalada precisa ser demonstrada. Para ver o enunciado da proposição e sua demonstração clique aqui.

Função exponencial e progressões

   Seja $f : $ IR $ \to $ IR, $f(x) = ba^{x}$, uma função de tipo exponencial. Se $x_{1}$, $x_{2}$, ..., $x_{n}$, ... é uma progressão aritmética de razão $h$, isto é, $x_{n + 1} = x_{n} + h$, então os valores

$f(x_{1}) = ba^{x_{1}}$, $f(x_{2}) = ba^{x_{2}}$, ..., $f(x_{n}) = ba^{x_{n}}$, ...,

formam uma progressão geométrica de razão $a^{h}$, pois

$f(x_{n + 1}) = ba^{x_{n + 1}} = ba^{x_{n + h}} = (ba^{x_{n}}) \cdot a^{h}$.

   Como o (n + 1)-ésimo termo da progressão aritmética dada é $x_{n + 1} = x_{1} + nh$, segue-se que $f(x_{n + 1}) = f(x_{1}) \cdot A^{n}$, onde $A = a^{h}$. Em particular, se $x_{1} = 0$, então $f(x_{1}) = b$, logo $f(x_{n + 1}) = b \cdot A^{n}$.

Teorema 2

   Seja $f : $ IR $ \to $ IR₊ uma função monótona injetiva (isto é, crescente ou decrescente) que transforma toda progressão aritmética $x_{1}$, $x_{2}$, ..., $x_{n}$, ... numa progressão geométrica $y_{1}$, $y_{2}$, ..., $y_{n}$, ..., $y_{n} = f(x_{n})$. Se pusermos $b = f(0)$ e $a = \displaystyle\frac{f(1)}{f(0)}$ teremos $f(x) = ba^{x}$ para todo $x \in $ IR.

Demonstração: Seja $b = f(0)$. A função $g : $ IR $ \to $ IR₊, definida por $g(x) = \displaystyle\frac{f(x)}{b}$, é monótona injetiva, continua transformando progressões aritméticas em progressões geométricas e agora tem-se $g(0) = 1$. Dado $x \in $ IR qualquer, a sequência $x$, 0, $\mbox{-}x$ é uma progressão aritmética, logo $g(x)$, 1, $g(\mbox{-}x)$ é uma progressão geométrica de razão $g(\mbox{-}x)$. Segue-se $g(\mbox{-}x) = \displaystyle\frac{1}{g(x)}$. Sejam agora $n \in \mathbb{N}$ e $x \in $ IR. A sequência 0, $x$, $2x$, ..., $nx$ é uma progressão aritmética, logo 1, $g(x)$, $g(2x)$, ..., $g(nx)$ é uma progressão geométrica, cuja razão evidentemente é $g(x)$. Então seu (n + 1)-ésimo termo é $g(nx) = g(x)^{n}$. Se $\mbox{-}n$ é um inteiro negativo então $g(\mbox{-}nx) = \displaystyle\frac{1}{g(nx)} = \displaystyle\frac{1}{g(x)^{n}} = g(x)^{\mbox{-}n}$. Portanto, vale $g(nx) = g(x)^{n}$ para quaisquer $n \in \mathbb{Z}$ e $x \in $ IR. Considerando $a = g(1) = \displaystyle\frac{f(1)}{f(0)}$, tem-se $g(x) = a^{x}$, ou seja, $f(x) = ba^{x}$, para todo $x \in $ IR.

Obs.:

as demonstrações realizadas acima podem ser consultadas em Lima, E.L., Carvalho, P. C. P., Wagner, E. & Morgado, A. C. (2001) A Matemática do Ensino Médio. Coleção do Professor de Matemática. V. 1. Rio de Janeiro: Sociedade Brasileira de Matemática.

Hughes-Hallett, D., Gleason, A. M., Lock, P.  F., Flath, D. E. et al. (1999) Cálculo e Aplicações. São Paulo: Editora Edgard Blücher LTDA.

Kasner, E. e Newman, J. (1961) Mathematics and the Imagination. Londres: G. Bells and sons Ltd.

Lima, E.L., Carvalho, P. C. P., Wagner, E. & Morgado, A. C. (2001) A Matemática do Ensino Médio. Coleção do Professor de Matemática. V. 1. Rio de Janeiro: Sociedade Brasileira de Matemática.

Maor, E. (2003) E: a história de um número. Rio de Janeiro: Record.