|
Do you want to print the net of this polyhedron? Click here!
|
HOW TO USE THE APPLET?
|
|
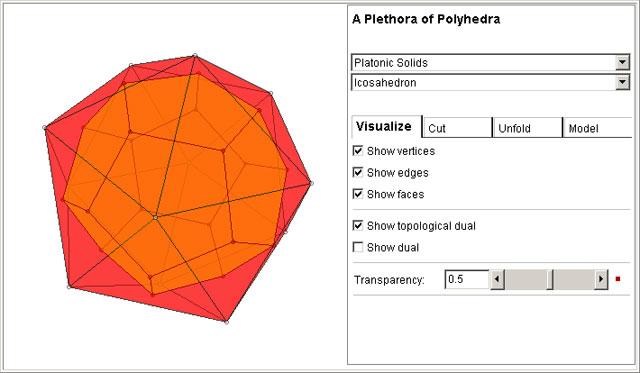
This is a free program that helps users to study spatial geometry in a dynamic and interactive way.
Using it, you can rotate, zoom out, zoom in and translate a plethora of polyhedra.
Moreover, the program is able to compute topological and geometrical duals of each polyhedron.
Geometrical operations include unfolding, plane sections, truncation and stellation.
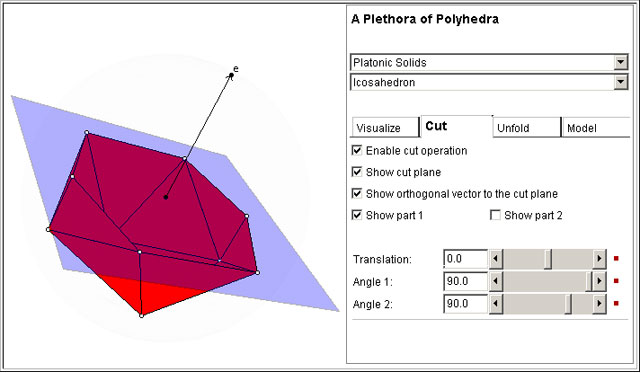
The Cut Tab has controls that allow the computation of plane sections. To use this feature, you must enable the operation first (click on the check box). To translate or rotate the cutting plane, just use the sliders. There is another way to rotate the cutting plane: keeping the key “i” pressed, click with the mouse left button over the polyhedron and, then, drag the mouse.
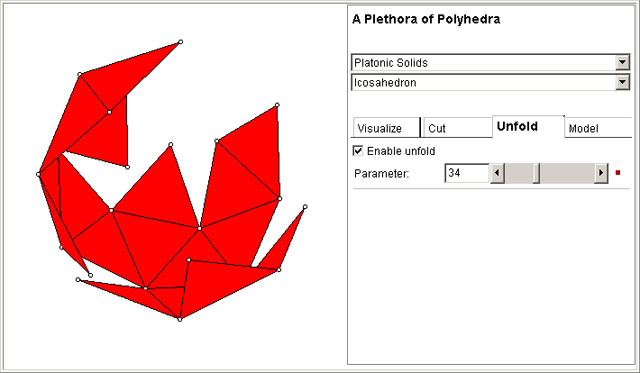
In the Unfold Tab, you can unfold the polyhedron. The slider configures the degree of deformation between the original polyhedron and its planar version.
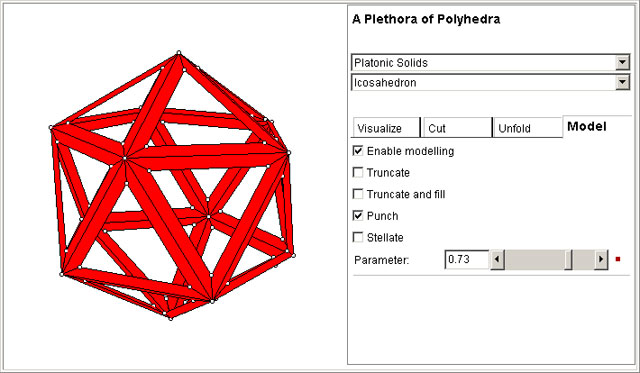
Finally, in the Model Tab, you can truncate, punch or stellate the polyhedron. The slider adjusts the strength of the operation.
To use the keyboard shortcuts listed below, first you have to click on the background where the polyhedron is shown.
|
|
SUPPLEMENTARY INFORMATION
|
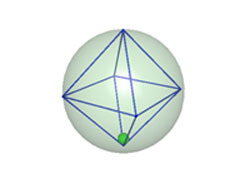
| THE ROUND DICE: A MANIFESTATION OF DUALITY | |||
|
It is possible to use the concept of duality to construct a round fair dice (that is, with a 1/6 probability for each one of the six values that can be drafted). The round dice markings are painted over the surface of a sphere using an analogous disposition of a conventional cube. Inside the sphere, there is a cavity with the shape of the cube dual, an octahedron. Inside the cavity, it is placed a small heavy metallic sphere that stays loose. When the round dice is rolled, the whole structure tends to balance itself with the small sphere occupying the position of one of the octahedron's six vertices and, therefore, the top of the spherical surface will present one of the six markings.
|
| UNFOLDING POLYHEDRA | ||||||||||
|
An unfolding of a polyhedron is the result of the process of
cutting the polyhedron along curves and, then, opening it in a way that it can be placed
over a plain surface, without overlaps and without faces deformations.
An unfolding by edges is the one obtained by cuts along the polyhedron edges.
Much more than artistic applications, the study of polyhedra unfolding has applications in industrial design (in the confection of vinyl molds and metallic plates decompositions). Nowadays, there are in the market softwares specialized in the computation of polyhedral surfaces unfoldings.
The regular tetrahedron has 2 different unfoldings.
The cube and the regular octahedron have 11 different unfoldings.
The regular icosahedron and the regular dodecahedron have 43380 different unfoldings.
It is not known if any convex polyhedron has an unfolding by edges. It is known, however,
that there are non-convex polyhedra that don't have such unfolding.
|
||||||||||
| THE EULER'S FORMULA | |||||
|
The great Swiss mathematician Leonhard Euler (1707–1783), on November 14th, 1750, wrote a letter to his friend (also a mathematician) Christian Goldbach (1690–1764) presenting a “general property of stereometry” that today, in his honor, is known as Euler’s Formula: if V, A and F are, respectively, the number of vertices, edges and faces of a polyhedron, then the formula holds for the class of polyhedra that are homeomorphic to a sphere (“homeo” = same, “morphous” = shape). 
Swiss stamp celebrating the 300 years of Euler's birth. Intuitively, if a polyhedron is homeomorphic to a sphere and if we consider that it is made of rubber, when air is injected in this polyhedron, it will deform into a sphere. Convex polyhedra are always homeomorphic to a sphere and there are non-convex polyhedra that are also homeomorphic to a sphere.
The polyhedron below is not homeomorphic to a sphere. If it was made of rubber, when air is injected in this polyhedron, it would deform into a torus (an object with the shape of a tire). 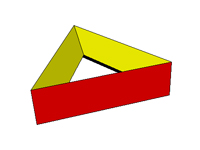
Example of a polyhedron not homeomorphic to a sphere (click on the image to access the 3D model). By the way, for polyhedra that are homeomorphic to a torus, the following equation holds: V − A + F = 0. More generally, for a polyhedron with G holes passing through it, it holds that: The numbers G and V − A + F are denominated, respectively, genus and Euler's characteristic of the polyhedron. It can be shown that if a polyhedron has genus G, then it is homeomorphic to a (hollow) sphere with G handles. To create a handle on a sphere, you just have to open two holes in it and glue a bended cylinder on them, as it is illustrated in the figure below. 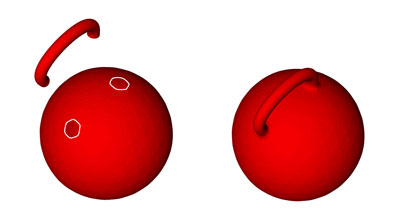
How to create a handle on a sphere. Other generalizations of Euler's formula that include other definitions of polyhedron can be found in the excellent article [Grünbaum & Shephard, 1994]. |
| FAIR DICE: ISOHEDRA |
|
When we roll a cubical dice made of a homogenous material, its symmetry grants that each one of its six faces have the same probability to stay on the top at the end of the rolling process (in this case, this probability is 1/6). Are there other convex polyhedra that could be used to build a fair dice? To answer this question, we have to look for convex polyhedra with the following property: any face can be carried to any other face by a rotation, a reflection or a composition of both, transforming the polyhedron into itself. Using algebra (group theory) and geometry, it is possible to show there are only 30 classes of polyhedra with this characteristic, the so called isohedra, available in the software of this activity. Five of these classes are infinite: triangular dihedron (2 n sides), basic trapezoidal dihedron (2 n sides), asymmetrical trapezoidal dihedron (2 n sides), asymmetrical triangular dihedron that moves points up/down (4 n sides), asymmetrical triangular dihedron that moves points in/out (4 n sides). 











Pictures: Alea Kybos’ Dice Collection. |
| COMPUTER GRAPHICS: POLYHEDRA AND SUBDIVISION SURFACES |
|
In Computer Graphics, polyhedra are used as a control mesh to model complex smooth surfaces. The final smooth surface is obtained through a recursive process that subdivides each polyhedron's faces into smaller subfaces. This technique was originally proposed by Ed Catmull (president and cofounder of Pixar Animation Studios) and James H. Clark. 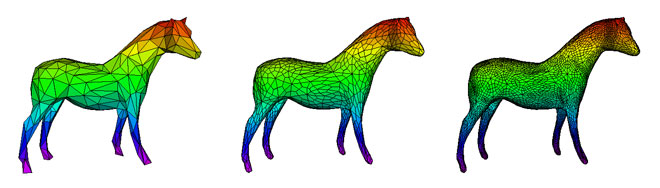
Refining the control mesh of a 3D model of a horse. |
|