Visualizar é uma das habilidades mais importantes para o desenvolvimento do aluno com relação aos conceitos da geometria espacial. Contudo, um professor típico dispõe (e usa) apenas o livro texto como ferramenta didática para o ensino deste assunto. Sendo mídias bidimensionais, a página de um livro ou o quadro-negro não são os instrumentos mais adequados para se treinar visualização. O emprego de materiais concretos se põe como uma excelente alternativa para explorar o assunto. Outra abordagem promissora é o uso de recursos computacionais: modelos tridimensionais podem ser manuseados virtualmente na tela de um computador, construindo assim uma ponte entre a representação planar (quando o sólido está estático na tela do computador) e o modelo concreto (quando o usuário interage com o sólido). Neste contexto, o objetivo desta atividade é criar uma pequena enciclopédia virtual interativa sobre os sólidos platônicos, apresentando suas propriedades matemáticas, os aspectos históricos, suas aplicações e modelos virtuais interativos.

A palavra poliedro tem sido usada em diferentes épocas por diferentes pessoas com os mais variados significados (muitas vezes, incompatíveis entre si). Não é raro que uma mesma pessoa use o mesmo termo com interpretações diferentes em momentos diferentes. Sem uma definição precisa, interpretações equivocadas (como, por exemplo, sobre a validade do Teorema de Euler) podem aparecer. Não nos deteremos nas nuances do significado da palavra. Para nossas necessidades, usaremos a seguinte definição de poliedro convexo:

Aqui nos restringiremos à classe de poliedros regulares:

Observe que o item (b) desta definição não segue de (a): as faces da bipirâmide pentagonal J13 (Figura 1), por exemplo, são triângulos equiláteros congruentes, mas o número de faces concorrentes em cada vértice não é sempre o mesmo.

Uma pergunta natural é se existe algum poliedro que satisfaz a Definição 2. Euclides inicia o Livro XIII de Os Elementos mostrando que existem pelo menos cinco deles: o tetraedro regular (Figura 2), o cubo ou hexaedro regular (Figura 3), o octaedro regular (Figura 4), o dodecaedro regular (Figura 5) e o icosaedro regular (Figura 6).

O sufixo edro vem da palavra grega hédra que significa face. Os prefixos, também oriundos do grego, indicam a quantidade de faces de cada poliedro: tetra (4), hexa (6), octa (8), dodeca (12) e icosa (20). A palavra cubo vem do latim cubu (estar deitado, estar estirado; repousar; estar deitado à mesa) e do grego kýbos.

Existem outros sólidos platônicos além destes cinco? A resposta é não! Apresentaremos aqui duas justificativas para este fato. A primeira, mais geométrica, segue a demonstração dada originalmente por Euclides. A segunda faz uso da fórmula de Euler.

Demonstração geométrica

Usaremos a seguinte propriedade fundamental: a soma dos ângulos dos polígonos em volta de cada vértice de um poliedro é sempre menor do que 360°. Esta é a proposição 21 do Livro XI do Os Elementos de Euclides. Apesar de intuitiva, a demonstração apresentada por Euclides é elaborada, sendo decorrente de uma sequência de resultados auxiliares [Joyce, 2008].

Vamos agora analisar as diversas possibilidades de união de faces em torno de cada vértice, lembrando que (1) em um sólido platônico as faces são polígonos regulares congruentes e (2) são necessárias pelo menos três faces unidas em cada vértice para formar um sólido.

1. As faces são triângulos equiláteros com ângulos internos de 60°. Temos as seguintes possibilidades:

2. As faces são quadrados com ângulos internos de 90°. Temos as seguintes possibilidades:

3. As faces são pentágonos regulares com ângulos internos de 108°. Temos as seguintes possibilidades:

4. Se as faces são polígonos regulares com n ≥ 6 lados, então a soma dos ângulos dos polígonos em torno de cada vértice é ≥ 360°. Sendo assim, não existe nenhum sólido platônico com faces hexagonais, heptagonais, etc.

Demonstração topológica

Daremos uma outra demonstração para o fato de que só existem cinco sólidos platônicos, usando agora a fórmula de Euler: se V é o número de vértices, A é o número de arestas e F é o número de faces de um poliedro convexo, então

Uma demonstração deste belíssimo resultado pode ser encontrada em [Lima, 1991]. A referência [Eppstein, 2008] apresenta 19 demonstrações diferentes para a fórmula de Euler (incluindo uma prova usando cargas elétricas).

Considere então um sólido platônico cujas faces são polígonos regulares de n lados. Como cada aresta do poliedro é definida pela interseção dos lados de dois polígonos adjacentes, segue-se que se contarmos todos os lados de todos os polígonos, iremos contar duas vezes cada aresta do poliedro. Desta maneira:

Denote por p o número de arestas do poliedro que concorrem em um mesmo vértice. Cada uma destas arestas, a exemplo das faces, se conecta a dois vértices. Assim, se contarmos o número de arestas em cada face, estaremos contando duas vezes o número de arestas do poliedro. Portanto:

Substituindo-se os valores de V e F das Equações (1.2) e (1.3) na Equação (1.1), teremos que 2 • A/p − A + 2 • A/n = 2 ou, ainda, 1/p − 1/A + 1/n = 1/2. Consequentemente,

Como o número A de arestas deve ser positivo, temos que 2 • n + 2 • p − n • p > 0, ou seja,

Uma vez que p ≥ 3, concluímos que, obrigatoriamente, n < 6. As possibilidades são então as seguintes:

Os gregos antigos estudaram os sólidos platônicos exaustivamente. Algumas fontes, como Proclo (410-485), atribuem a descoberta destes sólidos a Pitágoras (572 a.C.-497 a.C.). Outras evidências, contudo, sugerem que Pitágoras conhecia apenas o tetraedro, o cubo e o dodecaedro, enquanto que a descoberta do octaedro e do icosaedro é atribuída a Teeteto (417 a.C.-369 a.C.), que também conduziu um estudo mais aprofundado dos cinco sólidos regulares, incluindo a primeira demonstração conhecida de que existem somente cinco destes sólidos.

Os nomes sólidos platônicos ou corpos cósmicos foram dados devido a forma pela qual Platão (427 a.C.-34 a.C.), em um diálogo intitulado Timeu, os empregou para explicar a natureza. Não se sabe se Timeu realmente existiu ou se Platão o inventou como um personagem para desenvolver suas idéias. Em Timeu, Platão associa cada um dos elementos clássicos (terra, ar, água e fogo) com um poliedro regular. Terra é associada com o cubo, ar com o octaedro, água com o icosaedro e fogo com o tetraedro. Com relação ao quinto sólido platônico, o dodecaedro, Platão escreve: “Faltava ainda uma quinta construção que o deus utilizou para organizar todas as constelações do céu.”. Aristóteles introduziu um quinto elemento, éter, e postulou que os céus eram feitos deste elemento, mas ele não teve interesse em associá-lo com o quinto sólido de Platão.

Euclides deu uma descrição matemática completa dos sólidos platônicos no último livro (Livro XIII) de Os Elementos. As proposições de 13 a 17 no Livro XIII descrevem as construções do tetraedro, do octaedro, do cubo, do icosaedro, e do dodecaedro, nesta ordem. Para cada sólido, Euclides calcula a razão entre o diâmetro da esfera circunscrita e o comprimento da aresta do sólido. Na proposição 18, ele demonstra que não existem outros poliedros regulares. Muita da informação no Livro XIII é provavelmente obtida do trabalho de Teeteto.

No século XVI, o astrônomo alemão Johannes Kepler (1571-1630) tentou encontrar uma relação entre os cinco sólidos e os seis planetas que eram conhecidos na época: Mercúrio, Vênus, Terra, Marte, Júpiter e Saturno.

Figura 8: Johannes Kepler (1571-1630).

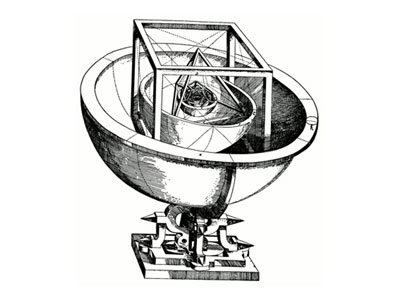
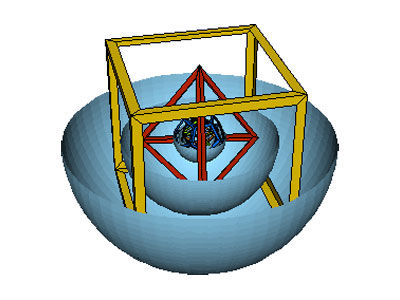
Kepler pensou que os dois números estavam conectados, isto é, que a razão pela qual havia somente seis planetas era porque existiam somente cinco sólidos regulares. Em 1596, em sua obra Mysterium Cosmographicum, Kepler estabeleceu um modelo do sistema solar onde os cinco sólidos platônicos eram colocados um dentro do outro, separados por uma série de esferas inscritas, na seguinte ordem: primeiro o octaedro seguindo-se o icosaedro, o dodecaedro, o tetraedro e, finalmente, o cubo. Ele conjecturou que as razões entre os raios das órbitas dos planetas coincidiam com as razões entre os raios das esferas. Seu modelo, contudo, não era sustentado pelos dados experimentais dos astrônomos Tycho Brahe (dinamarquês, 1546-1601) e Nicolau Copérnico (polonês, 1473-1543).

Figura 9: O modelo do sistema solar idealizado por Kepler.

Seu Mysterium Cosmographicum foi desaprovado por inteiro pelas descobertas posteriores dos planetas Urano, Netuno e Plutão: não há sólidos platônicos adicionais que determinem suas distâncias ao Sol. Por fim, Kepler abandonou o seu modelo. Contudo, de sua pesquisa, nasceram a descoberta de novos sólidos (que hoje, levam o seu nome), a percepção de que as órbitas dos planetas não são círculos (mas, sim, elipses) e as leis do movimento planetário.

Figura 10: Um modelo concreto do sistema solar idealizado por Kepler (Technisches Museum, Viena, Áustria). Foto: Sam Wise.

Figura 11: Um modelo 3D do sistema solar idealizado por Kepler (clique na figura).

Os sólidos platônicos se manifestam na natureza (cristais, organismos vivos, moléculas, etc.) e na cultura humana (pinturas, esculturas, religião, arquitetura, design, etc.).

Por exemplo, são muitas as formas cristalinas naturais no formato do tetraedro (calcopirita), do hexaedro (galena) e do octaedro (magnetita).

(a) calcopirita	(b) galena	(c) magnetita

Existe um cristal com doze faces pentagonais e três arestas saindo de cada um de seus vinte vértices: a pirita. Contudo, suas faces não são regulares.

Figura 13: Pirita. Crédito da foto: Roger Weller/Cochise College.

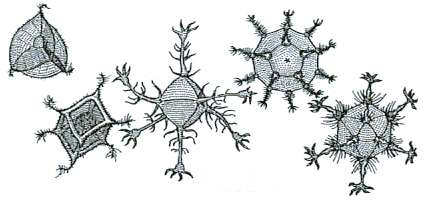
Em 1904 o biólogo alemão chamado Ernst Haeckel escreveu a obra Kunstformen der Natur descrevendo os radiolários, Figura 13, um tipo de protozoário ameboide que podem assumir formas de poliedros regulares. Podemos citar como exemplos o Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus e Circorrhegma dodecahedra.

Figura 14: Radiolários.

Muitos vírus, como o vírus da herpes, assumem a forma de um icosaedro regular. As estruturas virais são constituídas de subunidades protéicas idênticas repetidas e o icosaedro é a forma mais simples de se montar tais subunidades. Um poliedro regular é usado porque ele pode ser construído a partir de uma única unidade protéica básica e replicado várias vezes. Com isto, economiza-se espaço no genoma viral.

Em meteorologia e climatologia, destacam-se cada vez mais os modelos numéricos globais do fluxo atmosférico que usam malhas baseadas em um icosaedro (refinado por subdivisão) frente aos modelos que usam as coordenadas usuais de longitude e latitude.

Figura 15: Construção de uma malha icosaédrica e de sua malha dual.