|
Em 1612, o astrônomo alemão Johannes Kepler (1571-1630) mudou-se para Linz na Áustria.
A safra de vinho foi excelente naquele ano e o produto era vendido a um baixo preço.
Nas palavras do próprio Kepler:
|
“Depois de meu casamento em novembro do último ano, na época em que barris de vinho da
Baixa Áustria eram armazenados às margens do Danúbio perto de Linz após uma
safra abundante, sendo ofertada a um preço razoável, era dever do
novo marido e devotado pai de família comprar a bebida para consumo em seu lar.
Quatro dias depois, vários barris foram trazidos para a adega e o vendedor
de vinho veio com uma vareta que ele usou para medir a quantidade de vinho
em todos os barris, independentemente da sua forma e sem qualquer cálculo
ou estimativa adicionais. A extremidade metálica da vareta graduada era
introduzida pelo buraco no meio do barril até alcançar sua borda inferior.
[...] Surpreendeu-me que a diagonal colocada através da metade do barril pudesse
ser usada para se medir o volume, e eu duvidei da validade deste método, uma vez
que um barril menor com um fundo mais amplo e, então, com um volume menor,
poderia ter a mesma marcação na vareta graduada.
Para mim, como um recém-casado, não me pareceu inoportuno investigar
o princípio matemático por de trás dessa regra prática e amplamente usada para se medir
volumes e trazer luz às leis geométricas subjacentes.”

Ilustração de Johann Frey publicada em 1531 em Nuremberg.
|
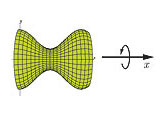
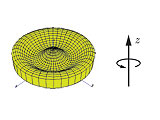
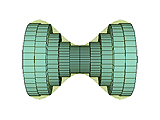
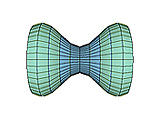
Um barril de vinho pode ser modelado como um sólido de revolução. Uma das ideias
de Kepler para calcular o volume do barril foi a de aproximá-lo por uma
sequência de troncos de cilindros justapostos, seguindo o mesmo princípio
apresentado na Parte 3 desta atividade.
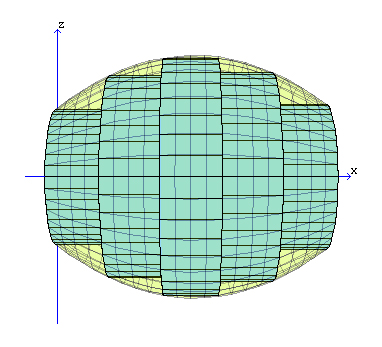
Kepler aplicou esta técnica para outros tipos de sólidos de revolução (92 no total).
Alguns destes sólidos já foram discutidos por Arquimedes (conóides e esferóides),
mas muitos outros eram novos. Para estes, Kepler deu esses nomes tais como maçã, limão, pera, noz, etc.
Seus estudos foram publicados no livro
Nova Stereometria Doliorum Vinariorum (Nova Estereometria de um Barril de Vinho) em 1615.
Muitos acadêmicos consideram este trabalho de Kepler como um dos marcos que antecedem a criação
do Cálculo Diferencial e Integral.


Fotos: páginas 33 e 98 do livro Nova Stereometria Doliorum Vinariorum de Kepler (Posner Memorial Collection in Electronic Format).
|