
Role a página 
| DESAFIOS |
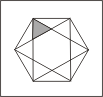
| 1º DESAFIO - A área do hexágono regular ABCDEF é 45 cm². Qual a área do triângulo sombreado (ver Figura a)? A) 2,0 cm²; B) 2,5 cm²; C) 3,0 cm²; D) 3,5 cm²; E) 4,0 cm². |
|
|
| Questão apresentada na Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP) de 2007. | ||
| 2º DESAFIO - Você seria capaz de, utilizando recursos da Geometria Dinâmica, construir uma animação eletrônica que modele trapézios de mesma área? |
3º DESAFIO -
Um agricultor deseja adquirir um terreno de pequeno porte numa região à beira de um rio. A região na qual se encontram os terrenos possui forma de trapézio, medindo 200 metros ao longo da estrada e 300 metros ao longo da margem do rio, conforme mostrado na Figura 1. A distância da estrada até a margem do rio é de 200 metros.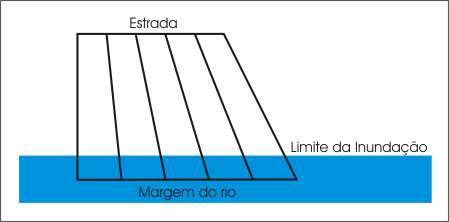 Figura 1 O agricultor precisa decidir qual dos cinco terrenos é o mais conveniente face ao fato de parte da região na qual se encontram os terrenos ser inundada periodicamente, impedindo o plantio. Ou seja, o agricultor precisa decidir qual dos terrenos possui a maior área cultivável. A linha da inundação dista 30 metros da margem do rio. Por não possuir outra forma de delimitar os terrenos, o seu proprietário dividiu os limites que confrontam a estrada e a margem do rio em cinco partes iguais e delimitou os terrenos a partir destas divisões conforme também mostrado na Figura 1. A) O agricultor pode comprar qualquer um dos terrenos ou deve se preocupar com a sua localização? B) E se os terrenos fossem retangulares ou tivessem outras formas de paralelogramos, qual deveria ser a preocupação do agricultor? |

 |




Responsável: |
Ana Maria Martensen Roland Kaleff. |
|
Idealização: |
Ana Maria Martensen Roland Kaleff e Bárbara Gomes Votto. |
|
Programação: |
Erick Baptista Passos e Manoel Mariano Siqueira Junior. |
|
Revisão: |
Ana Maria Martensen Roland Kaleff e Luana Sá de Azevedo. |
Elaborado no LEG - Laboratório de Ensino de Geometria da Universidade Federal Fluminense.
Polígonos Equivalentes Versão 20/03/2010
Possíveis atualizações e extensões desta atividade estarão disponíveis no endereço http://www.uff.br/cdme/.
Site alternativo: http://www.cdme.im-uff.mat.br.
conteudosdigitais@im.uff.br.
 Quer conferir suas respostas?
Quer conferir suas respostas?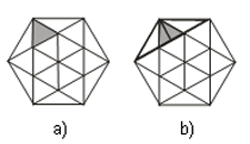
 Fechando Ideias...
Fechando Ideias...