Para realizar as atividades que se seguem você vai precisar:

a) Tome um pedaço de barbante com cerca de 15 cm. Coloque uma folha de papel em branco na Prancheta de Apoio, prenda o barbante com dois percevejos de forma que a distância entre eles seja um pouco menor que o comprimento barbante. Coloque um lápis no laço do barbante e desloque-o partindo de um ponto e retornando até ele, de modo a manter o barbante bem esticado sobre o papel. Como mostra a foto:

b) Observe a curva que foi desenhada, você já viu a forma desta curva antes? Você sabe qual é o nome dela? Agora você vai realizar uma tarefa para chegar à equação analítica da elipse. Para tanto, deve seguir a sequência de passos a seguir: c) Considere o desenho da elipse que você obteve. Com a régua, trace um segmento de reta passando pelos pontos onde foram fixados os percevejos. Chame esses pontos de F1 e F2. Saiba que eles são chamados de focos da elipse. d) Com régua e compasso trace a mediatriz do segmento de reta F1F2. Indique o ponto determinado pela interseção por O. Ele irá representar a origem de um plano cartesiano. Trace segmentos maiores que representem as retas suportes dos dois segmentos anteriormente traçados. Divida ambos em pequenos segmentos iguais e determine um sentido em cada um, para que ambos possam representar os eixos x e y do plano cartesiano.

Foto do Acervo do LEG.

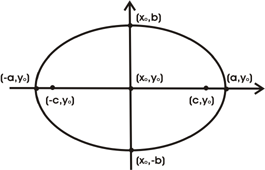
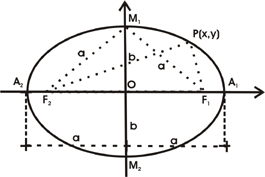
e) Chame o foco contido na parte positiva do eixo x de ponto F₁(c, 0) e o foco contido na parte negativa do eixo x de F₂(-c, 0).

f) Chame os pontos de interseção do eixo x com a curva de A₁(a, 0), ao ponto contido na parte positiva do eixo x, e A₂(-a, 0) ao contido na parte negativa do eixo x.

g) Chame os pontos de interseção do eixo y com a curva de M₁(0, b), ao ponto contido na parte positiva do eixo y, e M₂(0, -b) ao contido na parte negativa do eixo y.

h) Considere um ponto P(x, y) qualquer na curva.

i) Para calcular analiticamente d(P, F₁) + d(P, F₂), considere que o comprimento do barbante utilizado para desenhar a curva tenha tamanho igual a 2a (sendo a um número real positivo). Logo, tem-se que d(P, F₁) + d(P, F₂) = 2a.

Desenvolva esta igualdade tentando retirar as raízes quadradas; para isso, você deve elevar ao quadrado ambos os lados da igualdade. Lembre que será mais simples se você deixar uma raiz de cada lado do sinal de igual. Se você não conseguiu realizar este cálculo, acompanhe a sequência a seguir.

Fechando ideias...     Observe que, de d(P, F1) + d(P, F2) = 2a. Tem-se que: √[(x - c)2 + y2] + √[(x + c)2 + y2] = 2a √[(x + c)2 + y2] = 2a - √[(x - c)2 + y2] Elevando ao quadrado ambos os membros, (x + c)2 + y2 = 4a2 - 4a√[(x - c)2 + y2] + (x - c)2 + y2. Desenvolvendo os quadrados e deixando de um lado apenas o termo que possui raiz: 4a√[(x - c)2 + y2] = 4a2 + x2 - 2cx + c2 - x2 - 2cx - c2. 4a√[(x - c)2 + y2] = 4a2 - 4cx. Simplificando pelo fator comum e elevando ao quadrado mais uma vez a2((x - c)2 + y2) = a4 - 2a2cx + c2x2. a2x2 - 2a2cx + a2c2 + a2y2 = a4 - 2a2cx + c2x2. a2x2 - c2x2 + a2y2 = a4 - 2a2cx + 2a2cx - a2c2 e (a2c2)x2 + a2y2 = a2(a2 - c2). Agora, observe que, de acordo com a Figura 2, como o triângulo F1OM1 é retângulo, então a2 = b2 + c2. Logo, utilizando essa relação para retirar o parâmetro c da última equação anterior e simplificando-a por a2 e em seguida por b2, obtenha uma outra equação que tem um dos membros igual a 1. Você deve ter chegado à equação: x2/a2 + y2/b2 = 1. Em Geometria, esta equação é conhecida como equação reduzida da elipse de centro na origem do plano cartesiano. Figura 1 Figura 2