|
PARA SABER MAIS!!! |
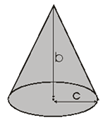
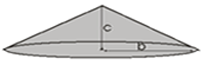
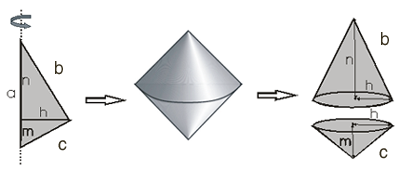
Você deve ter observado que neste conjunto de atividades não foi apresentado nenhuma relação entre áreas e entre volumes dos sólidos de revolução, pois o objetivo é levá-lo a aprimorar a sua habilidade da visualização e conseguir classificar esses sólidos. |
 |
|
|
||||

 |




Responsável: |
Ana Maria Martensen Roland Kaleff. |
|
Idealização: |
Ana Maria Martensen Roland Kaleff, Bárbara Gomes Votto e Luana Sá de Azevedo. |
|
Programação: |
Allan Carlos dos Santos, Erick Baptista Passos, Luciano Lucas de Oliveira Júnior e Manoel Mariano Siqueira Junior. |
|
Revisão: |
Ana Maria Martensen Roland Kaleff e Luana Sá de Azevedo.
|
Elaborado no LEG - Laboratório de Ensino de Geometria da Universidade Federal Fluminense.
Sólidos de Revolução Versão 20/03/2010
Possíveis atualizações e extensões desta atividade estarão disponíveis no endereço http://www.uff.br/cdme/.
Site alternativo: http://www.cdme.im-uff.mat.br.
conteudosdigitais@im.uff.br.
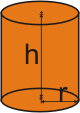
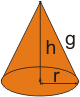
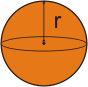
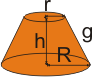
 Quer conferir as suas resposta?
Quer conferir as suas resposta?